Important questions class 12 physics electric charges and fields
- CH.PHYSICS

- Mar 25, 2020
- 8 min read
Updated: May 30, 2020
Electric Charges and Fields
[1 Mark Questions]
1. Why do the electrostatic field lines not form a closed-loop?
2. Why do the electric field lines never cross each other?
3. Why must the electrostatic field be normal to the surface at every point of a charged conductor?
4. Why must electrostatic field at the surface of a charged conductor be normal to the surface at every point? Give reason.
5. Two-point charges q1and q2are placed at a distance 'd’ apart as shown in the figure. The electric field intensity is zero at the point P on the line joining them as shown. Write two conclusions that you can draw from this.

6. Define the dipole moment of an electric dipole. Is it a scalar quantity or a vector quantity?
7. Draw a plot showing the variation of an electric field (E) with distance r due to a point charge Q.
8. A proton is placed in a uniform electric field directed along the positive X-axis. In which direction will it tend to move?
9. In which orientation, a dipole placed in a uniform electric field is in
i. stable and
ii. unstable equilibrium?
10. Two-point charges having equal charge separated by 1 m distance experience a force of 8 N. What will be the force experienced by them if they are held in the water at the same distance? (Given K water = 80).
11. A metallic sphere is placed in a uniform electric field as shown in the figure. Which path is followed by electric field lines and why?
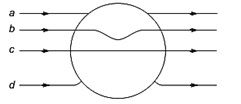
12. Point out right or wrong for the following statement.
The mutual forces between two charges do not get affected by the presence of other charges.
13. A dipole of dipole moment p is present in a uniform electric field E. Write the value of the angle between p and E for which the torque experienced by the dipole, is minimal.
14. Consider two hollow concentric spheres, S1 and S2, enclosingcharges2Qand 4Qrespectively as shown in the figure.
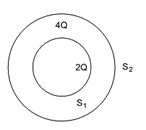
(i) Find out the ratio of the electric flux through them.
(ii) How will the electric flux through the sphere S1changeif a medium of dielectric constant ‘εr’ is introduced in the space inside S1inplace of air? Deduce the necessary expression.
15. Two charges of magnitude – 2Q and + Q are located at points (a, 0) and (4a, 0), respectively. What is the electric flux due to these charges through a sphere of radius 3awith its centre at the origin?
16. A charge q is placed at the centre of a cube of side l. What is the electric flux passing through each face of the cube?
17. The Figure shows three-point charges, + 2q, - q and +3q. Two charges+2qand – q are enclosed within a surface ‘S’. What is the electric flux due to this configuration through the surface ‘S’?
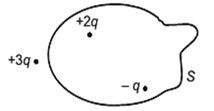
18. Define electric flux. Write its S.I. units.
19. A charge q is enclosed by a spherical surface of radius R. If the radius if reduced to half, how would the electric flux through the surface change?
20. State the Gauss law of electrostatics.
[2 Mark Questions] 1. An electric dipole of length 4 cm when placed with its axis making an angle of 60owith a uniform electric field, experiences a torque of 4√3 Nm. Calculate the potential energy of the dipole if it has a charge. 2. An electric dipole of length 2 cm when placed with its axis making an angle of 60o with a uniform electric field, experiences a torque of Nm. Calculate the potential energy of the dipole if it has charge of. 3. Two-point charges q and – 2qare kept d distance apart. Find the location of the point relative to charge q at which potential due to this system is zero. 4. An electric dipole is placed in a uniform electric field E with its dipole moment p parallel to the field. Find a. The work is done in turning the dipole till its dipole moment points in the direction opposite to E. b. The orientation of the dipole for which the torque acting on it becomes maximum. 5. Calculate the amount of work done in turning an electric dipole of dipole moment C-m from its position of unstable equilibrium to the position of stable equilibrium in a uniform electric field of intensity 103 N/C 6. Plot a graph showing the variation of Coulomb force (F) versus 1/r2, where r is the distance between the two charges of each pair of charges (1µC, 2µC) and (1µC,-3 µC). Interpret the graphs obtained. 7. Two identical metallic spherical shells A and B having charges +4Q and –10 Q are kept a certain distance apart. A third identical charged sphere C is first placed in contact with sphere A and then with sphere B, then spheres A and B are brought in contact and then separated. Find the charge on the spheres A and B. 8. A dipole with a dipole moment of magnitude p is in stable equilibrium in an electrostatic field of magnitude E. Find the work done in rotating this dipole to its position of unstable equilibrium. 9. A dipole is present in an electrostatic field of magnitude 106 N/C. If the work done in rotating it from its position of stable equilibrium to its position of unstable equilibrium is 2 x 10-23 J, then find the magnitude of the dipole moment of this dipole. 10. Deduce the expression for the electric field E due to a system of two charges q1andq2with position vectors r1 and r2at a point r with respect to a common origin. 11. A point charge causes an electric flux – 3 x 10-14 Nm2/C to pass through a spherical Gaussian surface.
i. Calculate the value of the point charge.
If the radius of the Gaussian surface is double, how much flux would pass through the surface 12. Two charges +Q and – Q are kept at points (-x2,0) and (x1,0) respectively, in the XY – plane. Find the magnitude and direction of the net electric field at the origin (0,0) 13. Two-point charges 4Q and Q are separated by 1 m in the air. At what point on the line joining of charges, is the electric field intensity zero? 14. Given a uniform electric field N/C, find the flux of this field through a square of 10 cm on a side whose plane is parallel to the YZ – plane. What would be the flux through the same square if the plane makes an angle of 30owith the X-axis? 15. A thin straight infinitely long conducting wire having charge density λ is enclosed by a cylindrical surface of radius r and length l, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder. 16. Two charged conducting spheres of radii r1 and r2connected to each other by a wire. Find the ratio of electric fields at the surfaces of the two spheres. 17. Show that the electric field at the surface of a charged conductor is given by, where is the surface charge density and is the unit vector normal to the surface in the outward direction. 18. A spherical conducting shell of inner radius R1and outer radius R2has a charge Q. A charge q is placed at the centre of the shell. i. What is the surface charge density on the
a. Inner surface, b. The outer surface of the shell. ii. Write the expression for the electric field at a point to x>R2from the centre of the shell.
19. Draw the spheres of the suitable Gaussian Surfaces while applying Gauss’s law to calculate the electric field due to
i. A uniformly charged long straight wire.
ii. A uniformly charges infinite plane sheet.
20. A uniformly charges conducting sphere of 2.4 m diameter has a surface charge density of
80.0 µC/m2
i. Find the charge on the sphere.
ii. What is the total electric flux leaving the surface of the sphere?
21. Two large parallel thin metallic plates are placed close to each other. The plates have surface charge densities of opposite signs and of magnitude 2.0 x 10-12 C/m2. Calculate the electric field intensity
i. In the outer region of the plates
ii. In the interior region between the plates.
[3 Mark Questions]
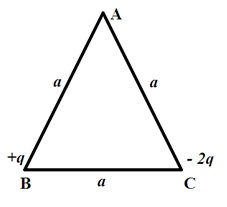
1. Two-point charges +q and – 2q are placed at the vertices B and C of an equilateral triangle ABC of the side as shown in the figure. Obtain the expression for
i. The magnitude and
ii. The direction
Of the resultant electric field at the vertex A due to these two charges.
2. Define the term electric dipole moment. Is it a scalar or vector? Deduce an expression for the electric field at a point on the equatorial plane of an electric dipole of length 2a.
3. Sketch the pattern of electric field lines due to
i. A conducting sphere having a negative charge on it.
ii. An electric dipole.
4. A positive point charge (+q) is kept in the vicinity of an uncharged conduction plate. Sketch electric field lines originated from the point on to the surface of the plate.
5. Using Gauss law, obtain the expression for the electric field due to uniformly charged spherical shell of radius R at a point outside the shell. Draw a graph showing the variation of the electric field with r, for r > R and r < R.
6. Use Gauss’ law to derive the expression for the electric field between two uniformly charged parallel sheets with surface charge densities and -, respectively.
7. State Gauss’ law in electrostatics. Using this law, derive an expression for the electric field due to a uniformly charged infinite plane sheet.
8. State Gauss’ law in electrostatics. Using this law derive an expression for the electric field due to a long straight wire of linear charge density λ C/m.






Comments